Gambar Konstruksi Geometris – Dalam gambar teknik sering ditemukan penggunaan konstruksi geometris. Konstruksi geometri terdiri dari garis, sudut, lingkaran, dan lain lain. Lalu apa fungsi konstruksi geometris? Apa saja jenisnya dan bagaimana cara membuatnya?
Fungsi konstruksi geometris adalah untuk menolong dalam menuntaskan gambar tehnik. Hal ini dikarenakan konstruksi geometris yang dapat menghasilkan wujud yang rapi dan akurat
Ada banyak jenis konstruksi geometris yang sering dipakai pada gambar tehnik. Tiap jenis konstruksi geometris disamakan dengan keperluan pada gambar tehnik. Jenis konstruksi geometris itu terbagi dalam segilima, segienam, garis tegak lempeng, dan lain-lain yang seringkali dgunakan pada gambar tehnik.
Cara membuat konstruksi geometris sesungguhnya benar-benar simpel. Dalam pemakaian konstruksi geometris ini dibutuhkan supaya tiap hasil gambar tehnik bisa optimal. Tentu saja menggambar dengan tehnik hasilnya akan lebih baik dibanding menggambar dengan prediksi.
Fungsi Konstruksi Geometris
Fungsi konstruksi geometris untuk menolong menyeselesaikan satu hal mengenai gambar tehnik. Maknanya konstruksi geometris sebagai salah satunya tehnik yang dibutuhkan supaya gambar tehnik bisa rapi serta lebih tepat atau akurat hingga gambar sesuai apa yang diharapkan dan seluruh orang baik perencana atau eksekutor bisa pahami gambar tehnik yang ada.
Jenis Konstruksi Geometris
Dalam konstruksi geometris ada banyak jenis yang hubungannya dalam matematika sebagai wujud ukuran dan status yang simetris. Berikut sebagai jenis konstruksi geometris yang dipakai pada gambar tehnik:
- Garis Tegak Lurus sebagai cara membagikan garis jadi dua sama panjang dengan memakai garis yang tegak lurus.
- Membagikan sudut sebagai cara membagikan dua pojok supaya sama besar satu dengan yang lain meskipun sudut tidak yang tercipta tidak teratur
- Membuat segi lima sebagai cara untuk membuat segi lima teratur yang semua seginya sama panjang.
- Membuat segi enam sebagai cara untuk membuat segi enam teratur yang semua seginya sama panjang.
- Buat elips sebagai cara untuk membuat elips yang teratur hingga rapi dan akurat.
Cara Membuat Konstruksi Geometris
Sesungguhnya membuat konstruksi geometris pada gambar tehnik benar-benar gampang. Cuman dalam prosesnya dibutuhkan kecermatan dan kesabaran hingga hasil yang didapat benar-benar akurat dan rapi. Berikut sebagai cara membuat konstruksi geometris:
1. Garis Tegak Lurus
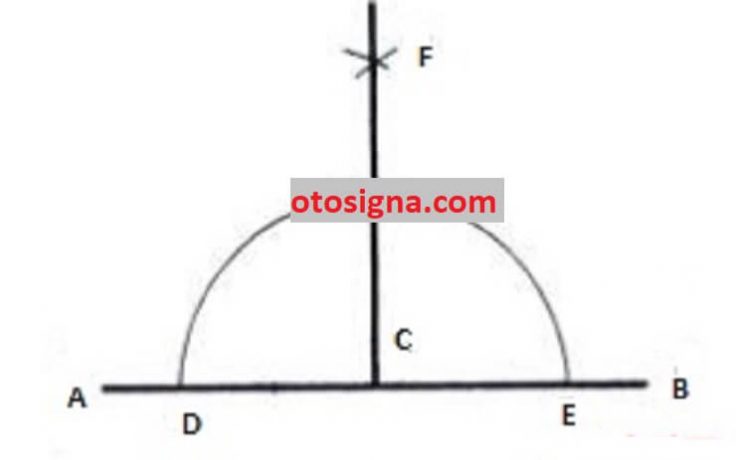
Untuk membuat garis tegak lurus sesungguhnya sangat gampang yakni dengan membuat garis lurus horisontal AB. Selanjutnya dengan memakai periode, buatlah lingkaran dengan titik tengah di titik A dan titik B hingga garis lingkarang sama-sama bergesekan. Bikinlah dua garis singgung dan berikan nama titik C dan titik D. Selanjutnya membuat garis dengan menarik secara lurus dimulai dari titik C sampai titik D hingga garis tegak lurus dan membagikan dua garis horisontal dengan akurat.
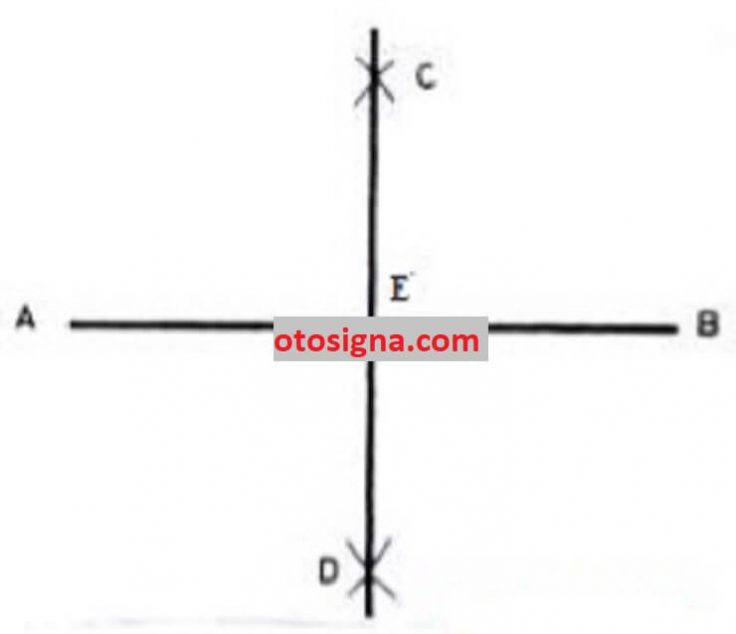
Untuk membuat garis tegak lurus yang cuman pada satu segi saja karena itu bisa dilaksanakan dengan cara membuat garis lurus horisontal AB. Berikan sandaran di titik tengah garis bernama C. Selanjutnya bikinlah 1/2 lingkaran dengan titik pijak di titik C. Berikan nama titik pada ujung 1/2 lingkaran D dan E. Selanjutnya tariklah garis memakai periode dari titik D dan titik E hingga bergesekan. Cara paling akhir ambil garis dari titik C dengan titik persinggungan yang ada.
2. Membagikan Sudut
Untuk membagikan sudut bisa dilaksanakan dengan langkah-langkah sebagai berikut ini:
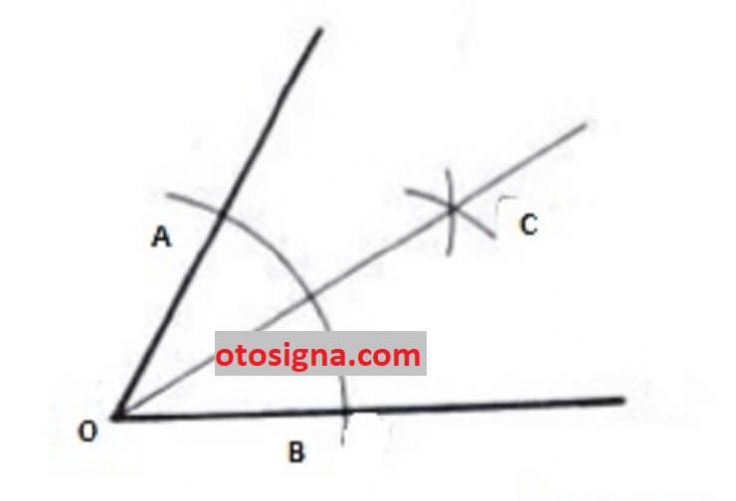
- Bikinlah lingkaran sampai menggunting pada dua garis sudut yang ada. Berikan nama titik A dan titik B.
- Selanjutnya dengan memakai alat jangka sorong, bikinlah lingkaran lewat titik A dan titik B sampai ke-2 nya bergesekan pada satu titik yang dinamakan titik C.
- Untuk memperoleh sudut yang serupa besar, maka tinggal menarik garis dimulai dari titik 0 sampai titik C. Sudut telah terdiri jadi dua sama besar.
3. Membuat Segilima
a Segilima Teratur
Membuat segilima sesungguhnya tidak begitu susah. Berikut sebagai cara untuk membuat segilima dengan panjang tiap seginya sama:
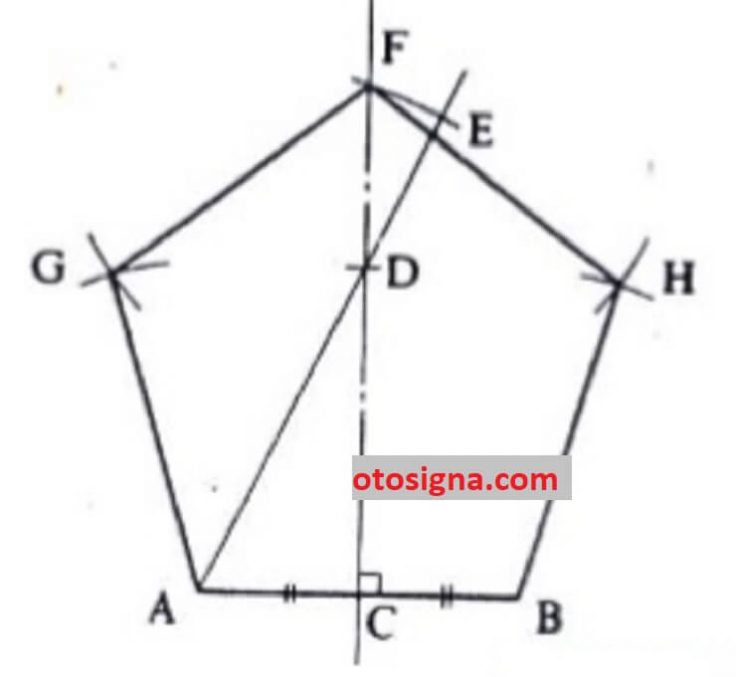
- Membuat garis horisontal AB selanjutnya dipisah jadi dua dengan garis tegak lurus. Sesudah didapat garis tegak lurus karena itu berikan nama titik C.
- Memakai alat jangka untuk membuat lingkaran dengan panjang jari-jari sama dengan panjang AB yang menggunting garis tegak lurus dan berikan nama titik D. Titik pijak lingkaran memakai titik A dan titik B hingga nanti didapat titik D yang disebut persinggungan dari ke-2 nya.
- Memakai alat jangka untuk membuat lingkaran dengan panjang jari-jari sama dengan AC atau BC sampai menggunting garis tegak lurus dan berikan nama titik F.
- Menggunakan alat jangka untuk membuat lingkaran dengan panjang jari-jari AB lewat titik F dan A hingga didapat titik dari persinggungan dua garis itu dan berikan nama titik G.
- Memakai alat jangka untuk membuat lingkaran dengan panjang jari-jari AB lewat titik F dan titik B hingga didapatkankkan titik dari persinggungan dua garis itu dan berikan nama titik H.
- Sambungkan titik A ke G, dari G ke F, dari F ke H, dan dari H ke B, hingga didapat segilima teratur.
b. Segilima Dalam Lingkaran
Sedang untuk membuat segilima dalam sebuah lingkaran harus lewat bermacam cara seperti berikut ini:
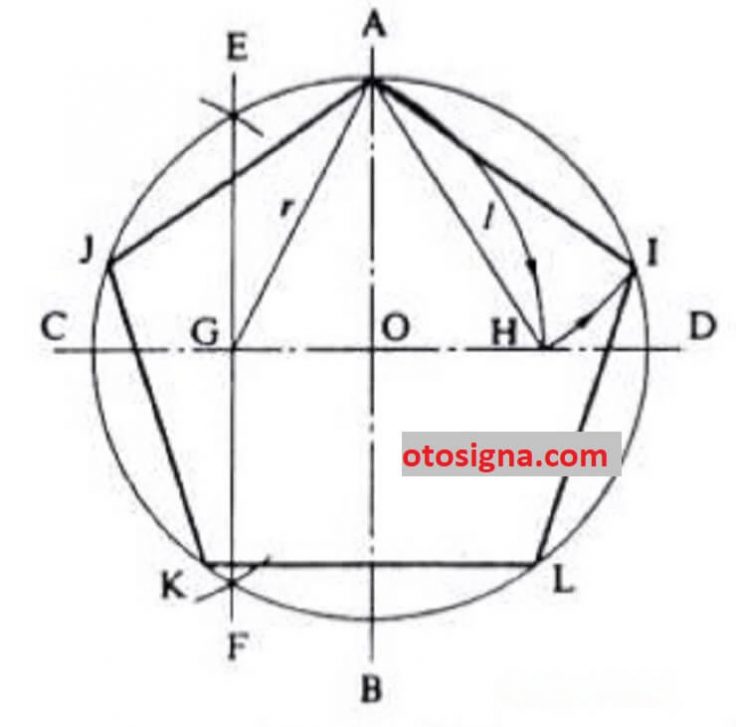
- Membuat sumbu AB dan CD lewat titik O.
- Untuk sama panjang CO, dengan cara melingkarkan jari-jari dari titik C dan O atas dan bawah didapat titik E dan F.
- Sambungkan titik E dan F, hingga didapat titik G. Dari titik G lingkarkan jari-jari r = GA didapat titik H.
- Mulai dari titik A lingkarkan jari- jemari l = AH, hingga didapat titik I dan J.
- Dari titik I lingkarkan jari-jari l didapatkan titik L, dan dari titik J didapat titik K, sambungkan garis dari titik A ke J, J ke L, L ke I, dan I ke A, hingga didapatkan segilima teratur AJKLI.
4. Membuat Segienam
a. Segi enam teratur
Membuat konstruksi geometris sisi enam sesungguhnya nyaris sama dengan membuat segilima teratur. Berikut sebagai cara membuat konstruksi geometris segienam:
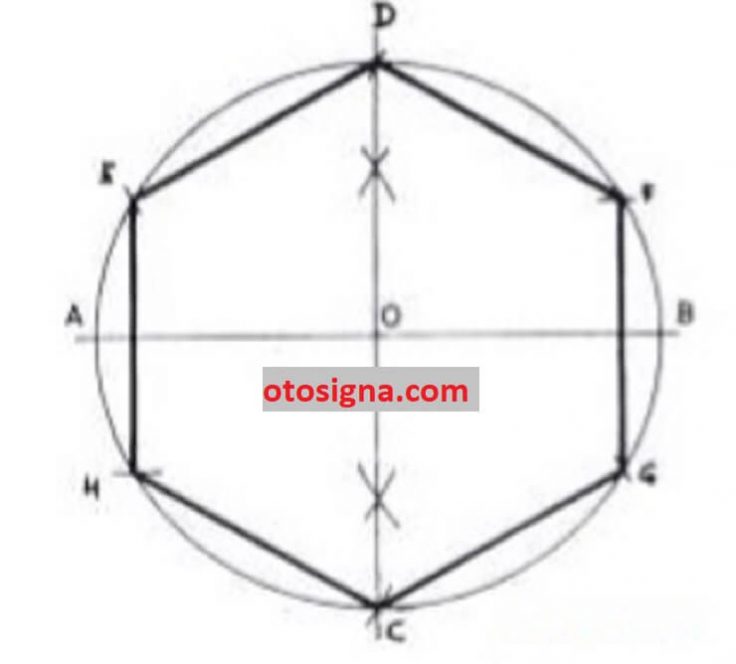
- Membuat sebuah lingkaran berdiameter AB.
- Buat garis tegak lurus dari garis AB lewat titik O.
- Selanjutnya berdiameter lingkaran yang sama dengan saat membuat lingkaran AB, bikinlah lingkaran dari titik D dan C hingga menggunting di titik E dan F, G dan H.
- Sambungkan beberapa titik D, E, G, C, G, F, dan D dengan garis lempeng hingga sama-sama tutup membuat sisi enam teratur.
b. Segienam Di Luar Lingkaran
Sedang untuk membuat segienam di luar lingkaran triknya hampir serupa dengan membuat segienam di dalam lingkaran yakni sebagai berikut ini:
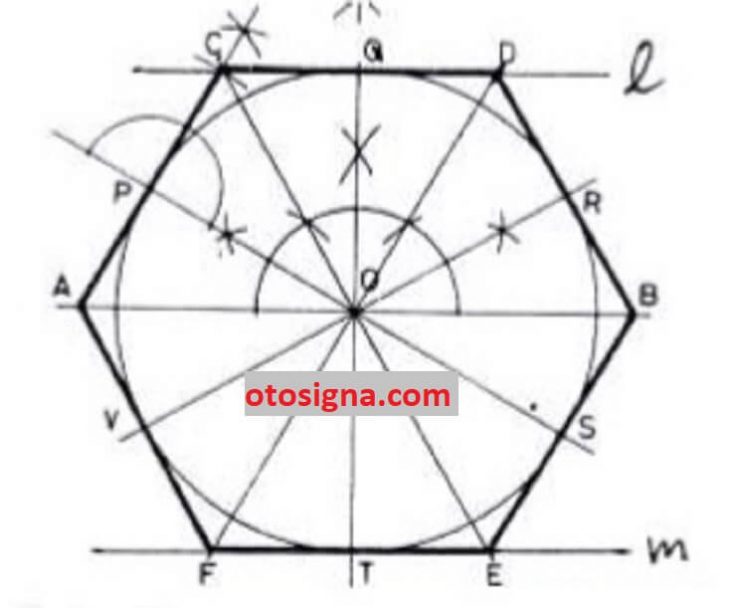
- Membuat lingkaran berdiameter AB.
- Buat garis tegak lurus dari garis AB dan berikan nama titik Q dan titik T.
- Membuat garis sejajar dengan AB lewat titik Q dan lewat titik T hingga didapat garis l dan m
- Dari titik pusat O buat pojok 30 derajat membuat pojok COQ dan QOD.
- Buat garis CE dan DF lewat titik pusat O.
- Sambungkan titik C dan D, dan titik F dan E hingga tercipta garis CD dan FE.
- Membuat garis dengan menyambungkan titik CA, FA, DB, dan EB yang menyentuh lingkaran di titik P, V, S, dan R.
- Sisi enam ACDBEF yang berada di luar lingkaran telah selesai.
5. Membuat Elips
Konstruksi geometris elips kecuali memerlukan tehnik memerlukan kreativitas dan seni sehinga saat menyambungkan antar titik menjadi satu garis yang sama-sama terkait satu dengan lain berupa elips. Berikut sebagai cara membuat elips:
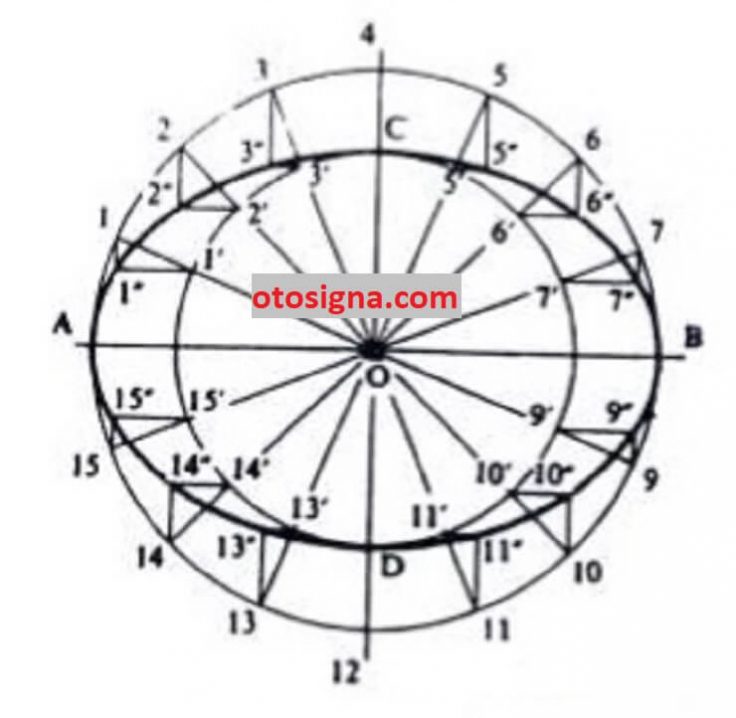
- Membuat dua buah lingkaran dengan jari-jari yang lain dari pusat sumbu yang serupa
- Bagilah lingkaran dengan sudut yang serupa, selanjutnya buat garis radial yang menggunting ke-2 lingkaran di titik 1, 2, 3, dstnya, 1‟, 2‟, 3‟, dstnya
- Membuat garis tegak lempeng dari titik 1, 2, 3 dstny
- Membuat garis sejajar dengan sumbu horisontal dari titik 1‟, 2‟, 3‟ dan sebagainya, hingga berpotongan di titik 1″, 2″, 3″, dan sebagainya
- Untuk membuat elips yakni dengan menyambungkan titik dari 1″, 2″, 3″… sampai titik 15″.
Selain itu memakai dua lingkaran yang berdiameter berlainan, membuat elips dapat lewat tolong persegi panjang. Berikut sebagai cara membuat elips memakai persegi panjang.
- Membuat sisi empat dengan sumbu-sumbunya.
- Pada sumbu OA bagilah jadi sama panjang dan dikasih notasi 1, 2, 3, dan 4. Dengan cara yang serupa pada segi AE dipisah jadi sama panjang dan dikasih notasi 1‟, 2‟, 3‟, dan 4‟.
- Buat garis lempeng dari titik C, hingga berkenaan garis AE di titik 1‟, 2‟, 3‟, dan 4‟. Dari titik D buat garis lempeng lewat titik 1, 2, 3, dan 4, hingga menggunting di titik 1″, 2″, 3″, dan 4″.
- Sambungkan titik 1″, 2″, 3″, dan 4″ hingga terbentu elips.
6. Menyentuh dua buah lingkaran
a. Persinggungan type 1
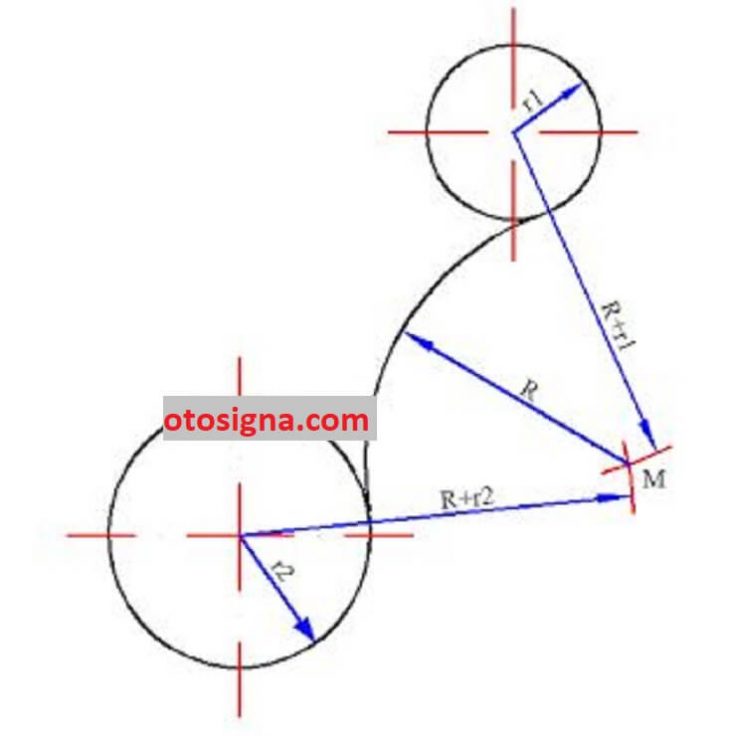
- Gambar busur – busur lingkaran dengan jemari – jemari R+r1 dan R+r2, masing – masing dengan titik tengah lingkaran 1 dana lingkaran 2 sebagai titik pusat. Ke-2 busur ini akan berpotongan di M
- Dengan titik M sebagai titik pusat buat busur yang ditanya dengan jemari – jemari R
b. Persinggungan type 2
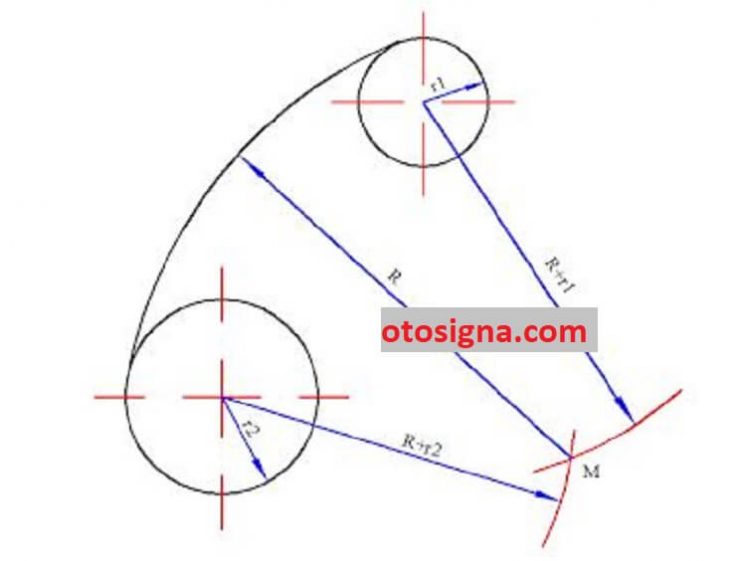
- Gambar busur – busur lingkaran dengan jemari – jemari R-r1 dan R-r2, masing masing dengan titik tengah lingkaran pertama dan ke-2 sebagai titik pusat. Ke-2 busur ini akan berpotongan di titik M
- Dengan titik M sebagai pusat bikinlah busur lingkaran yang ditanya dengan jemari – jemari R
7. Menyentuh dua buah garis
a. Garis yang sama-sama tegak lurus
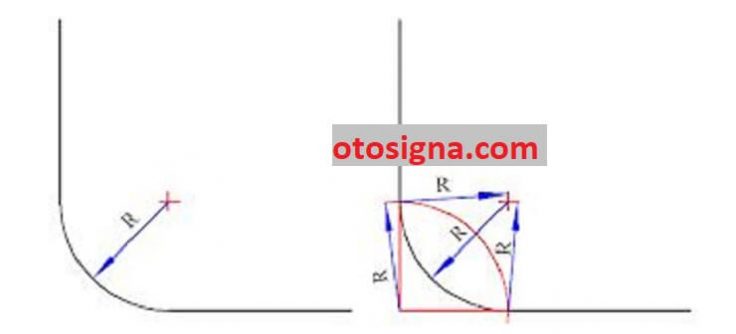
- Buat busur lingkaran dengan jemari – jemari R dan persinggungan sumbu vertical dan horizontal sebagai pusat hingga menggunting sumbu vertical dan horizontal
- Buat dua garis busur masing masing dengan jemari – jemari R dan titik pusat di titik perpotongan garis busur pertama dengan sumbu vertical dan horizontal
- Membuat busur dengan jemari – jemari R dan titik pusat di perpotongan dua garis busur awalnya sampai bergesekan dengan garis vertical dan horizontal
b. Garis yang berpotongan
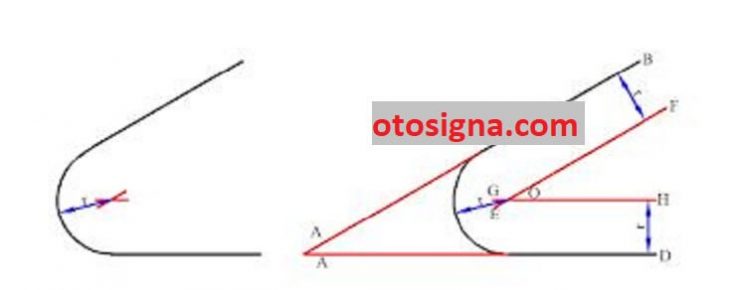
- Ambil garis EF dan GH yang masing – masing sejajar dengan AB dan CD, pada jarak r yang dijumpai
- Titik potong garis EF dan GH ialah titik O yang disebut pusat dari lingkaran singgung yang dicari
- Buat busur yang ditanya dengan radius r dan titik O sebagai titik pusat
Di atas sebagai ulasan berkenaan gambar konstruksi geometris. Ulasan terbagi dalam fungsi konstruksi geometris, jenis konstruksi geometris, dan cara membuat konstruksi geometris. Semoga menambah wawasan pengetahuan.



0 Komentar